硬件学习之数字电路(二)

因为上一章的图片太多了，所以分了一个第二部分章节

PS：个人感悟，学了一段时间的计算机底层知识，在我看来整个计算机从硬件到软件就是一个俄罗斯套娃，把一定功能的东西封装起来。使用者不需要知道其内里是如何实习的，只需要知道，我能输入什么，从而得到什么结果。

上一章学了一些逻辑门电路的实现，这章把逻辑门作为基本单元，来实现更复杂的元件。

半加器

半加器存在两个输入和两个输出端，两个输入表示需要相加的两个值，输出可以看成是表示加法结果。但是传统的说法为，一个是溢出位，一个结果。

逻辑如下表格：

inputA	inputB	Overflow C	result D
0	0	0	0
1	0	0	1
0	1	0	1
1	1	1	0

为什么结果要分成溢出位和结果位呢？我个人的想法是给容易理解逻辑电路的构成。

仔细看上面的表格，溢出位C的值其实就是输入A和B的与门结果。D的值就是异或的结果。

根据上面的理论，我们就能造出半加器了：

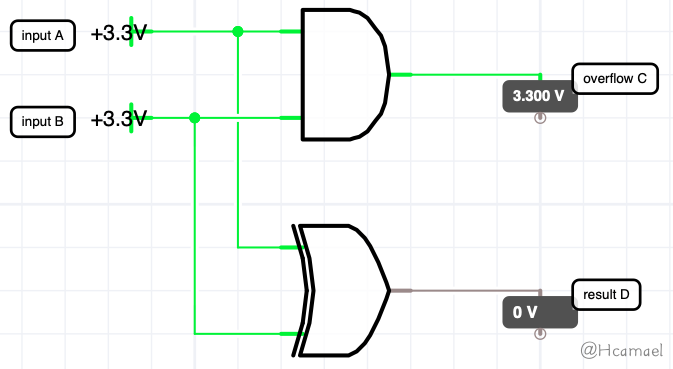
全加器

半加器的输出有两位，所以最多可以计算三位数相加的结果，所以有了全加器。我把半加器进行封装，然后构造出一个全加器：

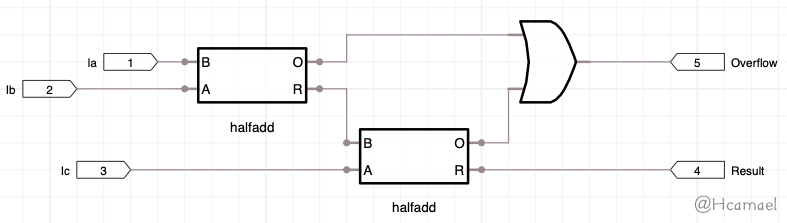
4位加法器

接下来我们可以再用封装的半加器和全加器做一个4位的加法器，4位加法器有8个输入，5位输出。如下图所示：

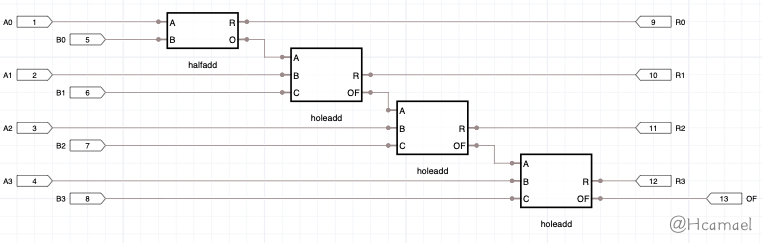
更高位的加法器只不过是增加更多的输入输出和全加器。

减法

有加自然要有减啊，那么有减法器吗？我想了下，应该是可以做，但是挺麻烦的。这个时候就是补码发挥作用的时候了，为啥要用补码这个设定？因为在底层只要设计加法器就能计算加减法。

补码规则：

正数补码 = 自身
负数补码 = not(self) + 1

比如在8bit的计算机中：

-14这个数的补码，14的二进制为0b00001110，取反得到0b11110001，加1得到0b11110010，所以-14的补码为0b11110010(242)，该值我们也可以看成是-14的无符号整数，如果要把该值再转化为有符号整数，首先看最高为，如果为0表示正数，值等于其本身，如果是1，表示符号，再重复一遍补码的计算：0b11110010->0b00001101->0b00001110

接下来我们来试试减法：24 - 17这个表达式我们可以看成24 + (-17)

-17的补码为0b11101111，24的补码为0b00011000，两者相加，得到0b00000111，忽略溢出位，最高位等于0，表示正数7。

再来举一个例子：-23-58，可以看成是(-23) + (-58)

-23的补码为0b11101001, -58的补码为0b11000110

进行加法计算，得到0b10101111，最高位为1，所以需要再算一遍补码，得到0b01010001，所以结果为-81。

对于计算机来说，所有数都可以看成是无符号整数，而补码的作用就是把无符号翻译成有符号整数。

搞完加减法，自然还有乘除法，乘法是通过循环+加法实现的，除法则是通过循环+减法实现的，等有空的时候，我再试着自己实现一下，再来补充本篇。

乘法

占位

除法

占位